Die Preisangabenverordnung (PAngV) stellt für Deutschland eine Vorschrift zur Berechnung des Effektivzinses bereit, danach muss der Effektivzins wie folgt berechnet werden:
$$\displaystyle\Large\sum_{K=1}^{K=m} \frac{A_{K}}{(1+i)^{t_K}} = \sum_{K^*=1}^{K^*=m^*} \frac{A^*_{K^*}}{(1+i)^{t^*_K{^*}}}$$
Einzelheiten, insbesondere eine Beschreibung der Formel können Sie hier nachlesen. Einer der wichtigsten Punkte ist: „Zugrunde gelegt werden für das Jahr 365 Tage, 52 Wochen oder 12 gleichlange Monate, wobei für letztere eine Länge von 365/12 Tagen = 30,416 Tagen angenommen wird.“ Dieser Sachverhalt ist schon daher sehr wichtig, weil in anderen Vorschriften zur Berechnung des Effektivzinses eine solche Annahme nicht oder in anderer Form vorgeschrieben wird.
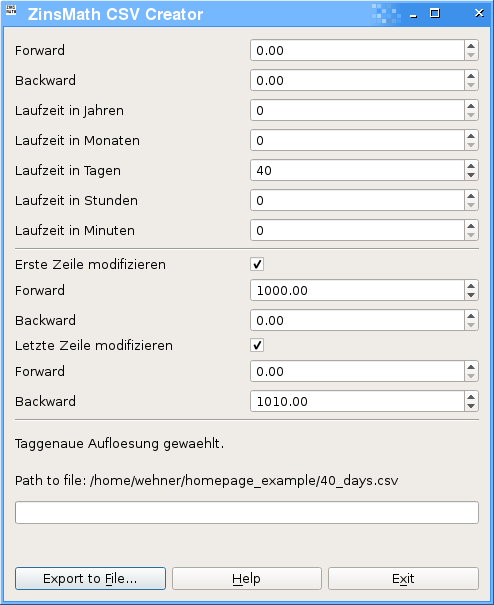
Aufgabe: Ein Darlehen über 1000 EUR wird für die Dauer von 40 Tagen ausgeliehen und in einer Rückzahlung über 1010 EUR ausgeglichen. Wie groß ist der Effektivzins / die Rendite des Projektes?
Zur Lösung dieser Fragestellung öffnen wir zunächst den ZinsMath CSV Creator und tragen die Zahlungen in den jeweiligen Feldern ein. Unter Forward verstehen wir dabei alle Zahlungen in ein Projekt und unter Backward verstehen wir alle Zahlungen, die aus dem Projekt entnommen werden. In der folgenden Abbildung sind die entsprechenden Daten zu sehen.
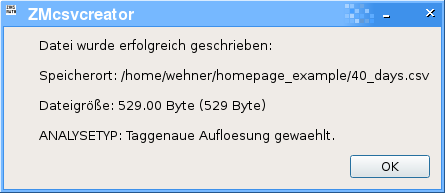
Nun wählen wir noch einen Ordner, in dem wir die Daten ablegen und schreiben den File:
Der Inhalt von 40_days.csv liegt nun im Text-Format vor und ist als CSV formatiert. Da wir hin und wieder auch etwas neugierig 🙂 sind, werfen wir einen Blick darauf und sehen folgende Struktur:
1000,00;0,00;0 0,00;0,00;1 0,00;0,00;2 0,00;0,00;3 0,00;0,00;4 0,00;0,00;5 usw... 0,00;0,00;37 0,00;0,00;38 0,00;0,00;39 0,00;1010,00;40
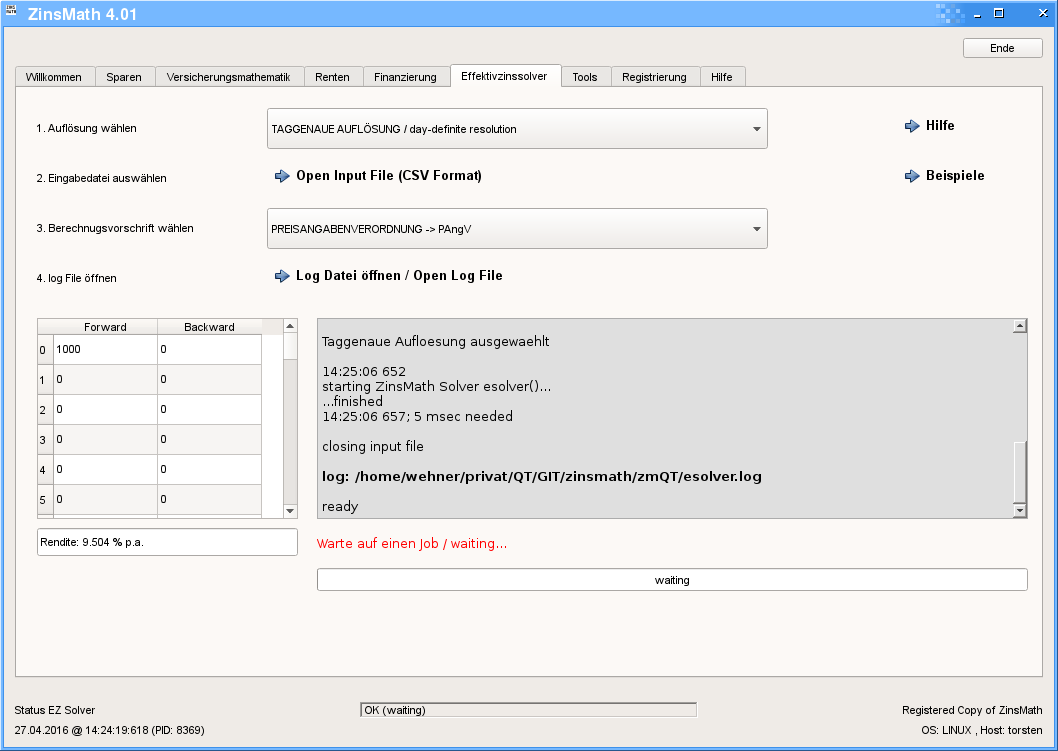
Nun öffnen wir das Menü des ZinsMath Effektivzinssolvers, wählen TAGGENAUE AUFLÖSUNG und öffnen den Input File.
![]()
![]() Sobald eine Input Datei erfolgreich gelesen werden konnte, wird die Berechnung sofort gestartet, der Effektivzins berechnet und das Ergebnis in Echtzeit sofort angezeigt. Bei jeder Berechnung wird eine LOG File generiert (esolver.log), der nicht nur die Ergebnisse beinhaltet, sondern auch weitere Informationen zum Dateninput, zum Konvergenzverhalten und zur Genauigkeit der Ergebnisse liefert.
Sobald eine Input Datei erfolgreich gelesen werden konnte, wird die Berechnung sofort gestartet, der Effektivzins berechnet und das Ergebnis in Echtzeit sofort angezeigt. Bei jeder Berechnung wird eine LOG File generiert (esolver.log), der nicht nur die Ergebnisse beinhaltet, sondern auch weitere Informationen zum Dateninput, zum Konvergenzverhalten und zur Genauigkeit der Ergebnisse liefert.
Mit einem Texteditor kann man natürlich auch hier einen Blick darauf werfen; das Ergebnis sieht in diesem Falle dann so aus:
27.04.2016
14:25:06
torsten
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
* * * *
* * * *
* * ZinsMath Effektivzinssolver * *
* * * *
* * * *
* * Torsten Wehner * *
* * Berthold-Haupt-Str. 22 * *
* * 01257 Dresden * *
* * wehner@zinsmath.de * *
* * * *
* * * *
* * Version 4.0 * *
* * 2013 * *
* * * *
* * * *
* * * *
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
You can find version-specific online documentation, and online technical
support at:
http://www.zinsmath.de
Welcome to Effektivzinssolver
numeric_limits(double) = 1.79769e+308
*C* INPUT DATA:
Increment = 365
Laufzeit = 40
*C* Anzahl der auf den Protokoll File geschriebenen Input Zeilen (maxlines):
maxlines = 50
*C* Echo:
0 Forward 1000.00 Backward 0.00
1 Forward 0.00 Backward 0.00
2 Forward 0.00 Backward 0.00
3 Forward 0.00 Backward 0.00
4 Forward 0.00 Backward 0.00
5 Forward 0.00 Backward 0.00
6 Forward 0.00 Backward 0.00
7 Forward 0.00 Backward 0.00
8 Forward 0.00 Backward 0.00
9 Forward 0.00 Backward 0.00
10 Forward 0.00 Backward 0.00
11 Forward 0.00 Backward 0.00
12 Forward 0.00 Backward 0.00
13 Forward 0.00 Backward 0.00
14 Forward 0.00 Backward 0.00
15 Forward 0.00 Backward 0.00
16 Forward 0.00 Backward 0.00
17 Forward 0.00 Backward 0.00
18 Forward 0.00 Backward 0.00
19 Forward 0.00 Backward 0.00
20 Forward 0.00 Backward 0.00
21 Forward 0.00 Backward 0.00
22 Forward 0.00 Backward 0.00
23 Forward 0.00 Backward 0.00
24 Forward 0.00 Backward 0.00
25 Forward 0.00 Backward 0.00
26 Forward 0.00 Backward 0.00
27 Forward 0.00 Backward 0.00
28 Forward 0.00 Backward 0.00
29 Forward 0.00 Backward 0.00
30 Forward 0.00 Backward 0.00
31 Forward 0.00 Backward 0.00
32 Forward 0.00 Backward 0.00
33 Forward 0.00 Backward 0.00
34 Forward 0.00 Backward 0.00
35 Forward 0.00 Backward 0.00
36 Forward 0.00 Backward 0.00
37 Forward 0.00 Backward 0.00
38 Forward 0.00 Backward 0.00
39 Forward 0.00 Backward 0.00
40 Forward 0.00 Backward 1010.00
*C* Memory information:
Vector size: 8 byte
Sum of forward elements: 328 byte
*C* Sum of input:
forward 1000
backward 1010
*C* Start of solution:
1 --- Fehler -- 115.322046
2 --- Fehler -- 29.848471
3 --- Fehler -- 20.415793
4 --- Fehler -- 15.203261
5 --- Fehler -- 11.638091
6 --- Fehler -- 8.947149
7 --- Fehler -- 6.795833
8 --- Fehler -- 5.009596
9 --- Fehler -- 3.486141
10 --- Fehler -- 2.160507
11 --- Fehler -- 0.988938
12 --- Fehler -- -0.059402
13 --- Fehler -- 0.988938
14 --- Fehler -- 0.878984
15 --- Fehler -- 0.770230
16 --- Fehler -- 0.662652
17 --- Fehler -- 0.556226
18 --- Fehler -- 0.450928
19 --- Fehler -- 0.346736
20 --- Fehler -- 0.243628
21 --- Fehler -- 0.141582
22 --- Fehler -- 0.040579
23 --- Fehler -- -0.059402
24 --- Fehler -- 0.040579
25 --- Fehler -- 0.030535
26 --- Fehler -- 0.020501
27 --- Fehler -- 0.010478
28 --- Fehler -- 0.000465
29 --- Fehler -- -0.009538
30 --- Fehler -- 0.000465
31 --- Fehler -- -0.000536
32 --- Fehler -- 0.000465
33 --- Fehler -- 0.000365
34 --- Fehler -- 0.000265
35 --- Fehler -- 0.000164
36 --- Fehler -- 0.000064
links 1000.000000
rechts 1000.000644
Abbruchkriterium 0.000100
Effektivzins in % p.a. 9.50
9.504000
Elapsed time (milliseconds): 1
Number of outer Loops: 36
Number of inner Loops: 72
Nothing to do: 1404
ZinsMath Effektivzinssolver run ended without errors
14:25:06
Der Effektivzins für dieses Projekt beträgt also 9,5 %. p.a. (pro Jahr).